What distance will a vehicle travel before coming to a complete stop from a speed of 70 mph, (a) When the vehicle is traveling on a level ro

Question

What distance will a vehicle travel before coming to a complete stop from a speed of 70 mph, (a) When the vehicle is traveling on a level roadway with no grade, (b-1) When the vehicle is traveling uphill on a roadway of constant grade = 0.10, (b-2) If the roadway grade is not constant but starts at 0.10 uphill and decreases to 0 at a continuous rate, would the braking distance be equal to, greater than, or less than that in the case of a constant 0.10 uphill grade, (c) When the vehicle is traveling downhill on a roadway of constant grade = 0.10.

in progress 0
Euphemia 3 years 2021-07-16T03:12:29+00:00 1 Answers 6 views 0

Answers ( )

  1. Acacia
    0
    2021-07-16T03:14:00+00:00
    Reply

    Answer:

    (a), The SSD will be 723.9 ft.

    (b-1), The SSD will be 620.2 ft.

    (b-2), The SSD will be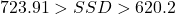 723.91>SSD>620.2

    (c), The SSD will be 910.5 ft.

    Explanation:

    Given that,

    Speed = 70 mph

    Suppose, a perception reaction time of 2.5 sec and the coefficient of friction is 0.35

    We need to calculate the stopping sight distance

    Using formula of SSD

    SSD=1.47\times v\times t+\dfrac{v^2}{30\times(f\pm g)}

    Where, v = speed of vehicle

    t = perception reaction time

    f = coefficient of friction

    g = gradient of road

    (a). If the gradient of road is zero.

    Then, the stopping sight distance will be

    SSD=1.47\times 70\times 2.5+\dfrac{70^2}{30\times(0.35)}

    SSD=723.9\ ft

    (b-1). If the gradient of road is 0.1

    Then, the stopping sight distance will be

    SSD=1.47\times 70\times 2.5+\dfrac{70^2}{30\times(0.35+0.1)}

    SSD=620.2\ ft

    (b-2). If the grade continuously decrease then the SSD will be increase.

    But if the grade is increase then the SSD will be decrease and for flat grade the SSD will be more.

    So, The SSD will be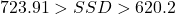 723.91>SSD>620.2

    (c). When the vehicle is traveling downhill on a roadway of constant grade then the vehicle take will be more SSD

    So, The SSD will be

    SSD=1.47\times 70\times 2.5+\dfrac{70^2}{30\times(0.35-0.1)}

    SSD=910.5\ ft

    Hence, (a), The SSD will be 723.9 ft.

    (b-1), The SSD will be 620.2 ft.

    (b-2), The SSD will be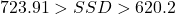 723.91>SSD>620.2

    (c), The SSD will be 910.5 ft.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )