The orbital radius of the Earth (from Earth to Sun) is 1.496 x 10^11 m. Mercury’s orbital radius is 5.79 x 10^10 m and Pluto’s is 5.91

Question

The orbital radius of the Earth (from Earth to Sun) is 1.496 x 10^11 m.
Mercury’s orbital radius is 5.79 x 10^10 m and Pluto’s is 5.91 x 10^12 m.
Calculate the time required for light to travel from the Sun to each of the
three planets.
a. Sun-Earth:_______
b. Sun-Mercury:________
c. Sun-Pluto:________​

in progress 0
Thu Thảo 3 years 2021-09-05T15:10:33+00:00 1 Answers 51 views 0

Answers ( )

  1. Tryphena
    0
    2021-09-05T15:11:55+00:00
    Reply

    Explanation:

    The orbital radius of the Earth is r_1=1.496\times 10^{11}\ m

    The orbital radius of the Mercury is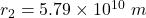 r_2=5.79 \times 10^{10}\ m

    The orbital radius of the Pluto is r_3=5.91 \times 10^{12}\ m

    We need to find the time required for light to travel from the Sun to each of the  three planets.

    (a) For Sun -Earth,

    Kepler’s third law :

    T_1^2=\dfrac{4\pi ^2}{GM}r_1^3

    M is mass of sun, M=1.989\times 10^{30}\ kg

    So,

    T_1^2=\dfrac{4\pi ^2}{6.67\times 10^{-11}\times 1.989\times 10^{30}}\times 1.496\times 10^{11}\\\\T_1=\sqrt{\dfrac{4\pi^{2}}{6.67\times10^{-11}\times1.989\times10^{30}}\times1.496\times10^{11}}\\\\T_1=2\times 10^{-4}\ s

    (b) For Sun -Mercury,

    T_2^2=\dfrac{4\pi ^2}{6.67\times 10^{-11}\times 1.989\times 10^{30}}\times 5.79 \times 10^{10}\ m\\\\T_2=\sqrt{\dfrac{4\pi^{2}}{6.67\times10^{-11}\times1.989\times10^{30}}\times 5.79 \times 10^{10}}\ m\\\\T_2=1.31\times 10^{-4}\ s

    (c) For Sun-Pluto,

    T_3^2=\dfrac{4\pi ^2}{6.67\times 10^{-11}\times 1.989\times 10^{30}}\times 5.91 \times 10^{12}\\\\T_3=\sqrt{\dfrac{4\pi^{2}}{6.67\times10^{-11}\times1.989\times10^{30}}\times 5.91 \times 10^{12}}\\\\T_3=1.32\times 10^{-3}\ s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )