The distribution of resistance for resistors of a certain type is known to be normal, with 10% of all resistors having a resistance exceedin

Question

The distribution of resistance for resistors of a certain type is known to be normal, with 10% of all resistors having a resistance exceeding 10.256 ohms and 5% having a resistance smaller than 9.671 ohms. What are the mean value and standard deviation of the resistance distribution? slader

in progress 0
Thu Hương 3 years 2021-08-24T23:22:41+00:00 1 Answers 121 views 0

Answers ( )

  1. King
    0
    2021-08-24T23:23:54+00:00
    Reply

    Explanation:

    Formula for the given probability is as follows.

               P(z > \frac{x - \mu}{\sigma}) = 0.10

           P(z > \frac{10.256 - \mu}{\sigma}) = 0.10

    According to the normal table area we have,

               P(z < 1.28) = 0.10

    Hence,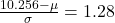  \frac{10.256 - \mu}{\sigma} = 1.28

                 \mu = 10.256 - 1.28 \times \sigma ………. (1)

    Also, the given probability is as follows.

               P(z < \frac{x - \mu}{\sigma}) = 0.05

              P(z < \frac{9.671 - \mu}{\sigma}) = 0.05

    Hence,     \frac{9.671 - \mu}{\sigma} = -1.645

                   \mu = 9.671 + 1.645 \times \sigma ……. (2)

    Now, substitute the value of \mu from equation (1) into equation (2) as follows.

          10.256 - 1.28 \times \sigma = 9.671 + 1.645 \times \sigma    

          -2.925 \sigma = -0.585

                 \sigma = 0.2

    Putting the value of \sigma into equation (2) we will find the value of \mu as follows.

                 \mu = 9.671 + 1.645 \times \sigma

                           = 9.671 + 1.645 \times 0.2

                           = 10

    Thus, we can conclude that the value of  \sigma is 0.2 and the value of \mu is 10.      

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )