What is the phase angle of an AC series circuit that is constructed of a 14.5-Ω resistor along with 16.5-Ω inductive reactance and 9.41-Ω ca

Question

What is the phase angle of an AC series circuit that is constructed of a 14.5-Ω resistor along with 16.5-Ω inductive reactance and 9.41-Ω capacitive reactance?

in progress 0
Minh Khuê 3 years 2021-09-02T23:38:07+00:00 2 Answers 7 views 0

Answers ( )

  1. Vodka
    0
    2021-09-02T23:39:20+00:00
    Reply

    Answer:

    26.06°

    Explanation:

    Given an RLC circuit [a circuit containing a capacitor, inductor and resistor], the phase angle (Φ), which is the difference in phase between the voltage and the current in the circuit, is given by;

    Φ = tan⁻¹ [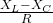 \frac{X_{L} - X_{C}}{R}]            ————————–(i)

    Where;

    X_{L} = inductive reactance of the circuit

    X_{C} = capacitive reactance of the circuit

    R = resistance of the circuit

    From the question;

    X_{L} = 16.5 Ω

    X_{C} = 9.41 Ω

    R = 14.5 Ω

    Substitute these values into equation (i) as follows;

    Φ = tan⁻¹ [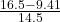 \frac{16.5 - 9.41}{14.5}]    

    Φ = tan⁻¹ [ \frac{7.09}{14.5}]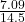

    Φ = tan⁻¹ [ 0.4890]

    Φ =  26.06°

    Therefore the phase angle of the AC series circuit is 26.06°

  2. mit
    0
    2021-09-02T23:39:43+00:00
    Reply

    Answer: cosθ = 0.7531

    Explanation: the phase angle cosθ is given as

    cosθ = R/Z

    Where R = resistive reactance = 14.5 ohms

    Z = impeadance = √R^2 +(Xl – Xc)^2

    Where Xl = inductive reactance = 16.5 ohms and Xc= capacitive reactance = 9.41 ohms

    By substituting the parameters, we have that

    Z = √14.5^2 + (16.5^2 – 9.41^2)

    Z = √210.25 + (272.25 – 88.5481)

    Z = √210.25 + 183.7019

    Z = √393.9519

    Z = 19.85 ohms

    Z = 19.85 ohms, R = 14.5 ohms

    cosθ = R/Z = 14.5/19.85

    cosθ = 0.7531

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )