Volume of a Cube The volume V of a cube with sides of length x in. is changing with respect to time. At a certain instant of time, the sides

Question

Volume of a Cube The volume V of a cube with sides of length x in. is changing with respect to time. At a certain instant of time, the sides of the cube are 7 in. long and increasing at the rate of 0.2 in./s. How fast is the volume of the cube changing (in cu in/s) at that instant of time?

in progress 0
Gerda 3 years 2021-09-03T01:36:12+00:00 1 Answers 22 views 0

Answers ( )

  1. mit
    0
    2021-09-03T01:38:10+00:00
    Reply

    Answer:

    Therefore the volume of cube is change at the 29.4 cube in./s at that instant time.

    Explanation:

    Formula

    • \frac{dx^n}{dx} =nx^{n-1}

    Cube :

    The volume of a cube is =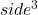 side^3

    The side of length is x in.

    Then volume of the cube is (V) =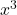 x^3

    ∴ V =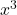 x^3

    Differentiate with respect to t

    \frac{d}{dt}(V)=\frac{d}{dt} (x^3)

    \Rightarrow \frac{dV}{dt} =3x^2\frac{dx}{dt}….(1)

    Given that the side of the cube is increasing at the rate of 0.2 in/s.

    i.e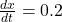 \frac{dx}{dt} = 0.2  in/s.

    And the sides of the cube are 7 in i.e x= 7 in

    Putting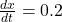 \frac{dx}{dt} = 0.2  and  x= 7 in equation (1)

    \therefore \frac{dV}{dt} =3 \times 7^2 \times 0.2  cube in./s

           =29.4 cube in./s

    Therefore the volume of cube is change at the 29.4 cube in./s at that instant time.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )