Vector 1 points along the z axis and has magnitude V1 = 80. Vector 2 lies in the xz plane, has magnitude V2 = 50, and makes a -37° angle wit

Question

Vector 1 points along the z axis and has magnitude V1 = 80. Vector 2 lies in the xz plane, has magnitude V2 = 50, and makes a -37° angle with the x axis (points below the x axis). What is the scalar product V1·V2?

in progress 0
Đan Thu 3 years 2021-08-17T14:15:13+00:00 1 Answers 9 views 0

Answers ( )

  1. thuhuong
    0
    2021-08-17T14:17:10+00:00
    Reply

    Answer:

    \vec{V1} . \vec{V2}  = 2574.08    

    Explanation:

    given data

    magnitude V1 = 80

    magnitude V2 = 50

    angle a =  -37°

    solution

    \vec{V1} = 80 k

    \vec{V2} = 50 cos{37} i  – 50sin{37} k

    so that here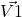 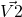\vec{V1} . \vec{V2}    is

    \vec{V1} . \vec{V2}  = 80 k . ( 50 cos{37} i  – 50sin{37} k )

    \vec{V1} . \vec{V2}  = 80 k . (  38.270 i + 32.176 k )

    \vec{V1} . \vec{V2}  = 2574.08    

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )