Share
Use equation I=∫r2dm to calculate the moment of inertia of a slender, uniform rod with mass M and length L about an axis at one end, perpend
Question
Use equation I=∫r2dm to calculate the moment of inertia of a slender, uniform rod with mass M and length L about an axis at one end, perpendicular to the rod. Express your answer in terms of the variables M and L.
in progress
0
Physics
3 years
2021-07-29T16:28:41+00:00
2021-07-29T16:28:41+00:00 1 Answers
360 views
0

Answers ( )
Answer:
The moment of inertia is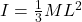
Explanation:
From the question we a given an equation
Now let look at a small length da of this uniform rod that a meters form the x-axis
The mass of this small section can be mathematically evaluated as
For this small portion for the rod the moment of inertia is
Substituting for dM
to get I we integrate both sides