Share
Two stars orbiting each other are separated by 6.67 AU and revolve around their common center of gravity in 10 years. Use Newton’s form of
Question
Two stars orbiting each other are separated by 6.67 AU and revolve around their common center of gravity in 10 years. Use Newton’s form of Kepler’s third law to calculate the combined mass of the 2 stars in solar masses.
in progress
0
Physics
3 years
2021-09-04T01:39:32+00:00
2021-09-04T01:39:32+00:00 1 Answers
4 views
0

Answers ( )
Answer:
The combined mass of the two stars is 2.9417 solar masses.
Explanation:
The mathematical expression for Kepler’s third law is;
Where: P is the period in days, a is the semimajor axis in AU,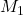 is the mass of the first star,
is the mass of the first star, 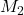 is the mass of the second star and k is the Gaussian gravitational constant.
is the mass of the second star and k is the Gaussian gravitational constant.
Given that;
P = 10 years = 3670 days (including two leap years)
a = 6.67 AU
k = 0.01720209895 rad
The sum of the masses of the two star can be determined by;
=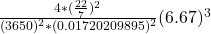
=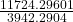
= 2.9417 solar masses
Thus the combined mass of the two star is 2.9417 solar masses.