Share
Two methods are proposed for testing a shipment of five items (call them A, B, C, D, and 13). In method 1, an inspector randomly samples two
Question
Two methods are proposed for testing a shipment of five items (call them A, B, C, D, and 13). In method 1, an inspector randomly samples two of the five items and tests to see whether either item is defective. In method 2, an inspector randomly samples one item and tests it; the remaining four items are sent to a second inspector who randomly samples one item and tests it. Suppose that only item A is defective in the shipment.
a. What is the probability that item A will be dis-covered by method 1?
b. What is the probability that item A will be dis-covered by method 2?
c. What general statement can you make regarding the effectiveness .of the two methods? Can your statement be extended to methods involving samples of more than two items?
in progress
0
Mathematics
3 years
2021-08-26T01:29:44+00:00
2021-08-26T01:29:44+00:00 1 Answers
13 views
0

Answers ( )
Answer:
a-The probability that item A is discovered as a defective item by method 1 is 0.4
b. The probability that item A is discovered as a defective item by method 2 is 0.4
c-As the probability of detecting A as a defective item is same for the two methods, thus it can be stated that each of the methods is equally effective.
Step-by-step explanation:
a-
The first method where the inspector chooses two of the five items randomly, so the total pairs are as given below:
As the total experiments in the overall space is 10 so is 10.
is 10.
As A comes in 4 of these experiments, thus the value of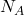 is 4.
is 4.
So the Probability of A is given as
The probability that item A is discovered as a defective item by method 1 is 0.4.
b-
Now in order to find the probability of finding item A as defective by method 2, first consider the probability of not finding item A as defective.
This is given as
Here P(A)’ is given as
Here
P(A)’_1st is the probability that the first inspector fails to detect A as a defective item which is given as
Here N_total items is 5. so the equation becomes
Similarly
P(A)’_2nd is the probability that the second inspector fails to detect A as a defective item which is given as
Here N_total items is 4 as 1 item has already been checked. so the equation becomes
So the main equation becomes
Substituting the values give
The probability that item A is discovered as a defective item by method 2 is 0.4.
c-
As evident from the above, that the value of probabilities for both the methods is same therefore the overall effectiveness of each of the methods is same.