Share
The mayor of a town has proposed a plan for the annexation of a new community. A political study took a sample of 900900 voters in the town
Question
The mayor of a town has proposed a plan for the annexation of a new community. A political study took a sample of 900900 voters in the town and found that 42B% of the residents favored annexation. Using the data, a political strategist wants to test the claim that the percentage of residents who favor annexation is above 388%. Find the value of the test statistic. Round your answer to two decimal places.
in progress
0
Mathematics
3 years
2021-09-04T16:09:21+00:00
2021-09-04T16:09:21+00:00 1 Answers
2 views
0

Answers ( )
Answer:
The value of the test statistic is 2.47.
Step-by-step explanation:
The test statistic is:
In which X is the sample mean, is the expected mean,
is the expected mean,  is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
For a proportion p, we have that:
A political study took a sample of 900 voters in the town and found that 42% of the residents favored annexation.
This means that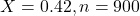
Using the data, a political strategist wants to test the claim that the percentage of residents who favor annexation is above 38%
This means that the expected is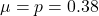
So
Find the value of the test statistic
The value of the test statistic is 2.47.