) (Problem 2.35 from text) Consider a light wave having a phase velocity of 3×10-8 m/s and a frequency of 6×1014 Hz. What is the shortest di

Question

) (Problem 2.35 from text) Consider a light wave having a phase velocity of 3×10-8 m/s and a frequency of 6×1014 Hz. What is the shortest distance along the wave between any two points that have a phase difference of 300

in progress 0
Kiệt Gia 3 years 2021-08-24T21:52:45+00:00 1 Answers 58 views 0

Answers ( )

  1. trucchi
    0
    2021-08-24T21:54:30+00:00
    Reply

    Answer:

    The shortest distance covered by the wave between the given points is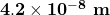 \bf{4.2 \times 10^{-8}~m}.

    Explanation:

    The Phase velocity (v_{p}) of any wave can be written as

    v_{p} = \dfrac{\omega}{k}

    where ‘\omega‘ is the angular velocity and ‘k‘ is the wave number.

    Also, if ‘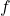f‘ is the frequency of the wave, then

    \omega = 2 \pi f

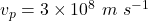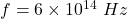    Given, v_{p} = 3 \times 10^{8}~m~s^{-1}, f = 6 \times 10^{14}~Hz and the phase difference between two points is \Delta \phi = 30^{0} = \dfrac{\pi}{6}.

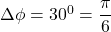    If the wave travels by the shortest distance of \Delta x between these points, then we can write

    && \Delta x \times k = \Delta \phi\\&or,& \Delta x = \dfrac{\Delta \phi}{k} = \dfrac{\Delta \phi v_{p}}{2 \pi f} = \dfrac{(\pi/6) v_{p}}{2 \pi f} = \dfrac{\pi v_{p}}{12 \pi f} = \dfrac{v_{p}}{12 f}\\&or,& \Delta x = \dfrac{3 \times 10^{8}~m~s^{-1}}{12 \times 6 \times 10^{14}~Hz} = 4.2 \times 10^{-8}~m

    \v_{p} = \dfrac{\omega}{k}[tex]\v_{p} = \dfrac{\omega}{k}[/tex]

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )