One of the wavelengths of light emitted by hydrogen atoms under normal laboratory conditions is at ?0 = 656.3nm in the red portion of the el

Question

One of the wavelengths of light emitted by hydrogen atoms under normal laboratory conditions is at ?0 = 656.3nm in the red portion of the electromagnetic spectrum. In the light emitted from a distant galaxy this same spectral line is observed to be Doppler-shifted to ? = 953.3nm , in the infrared portion of the spectrum.
How fast are the emitting atoms moving relative to the earth?

in progress 0
Thông Đạt 3 years 2021-07-29T01:08:23+00:00 1 Answers 18 views 0

Answers ( )

  1. ngocdiep
    0
    2021-07-29T01:10:12+00:00
    Reply

    Answer:

    1.07 × 10⁸ m/s

    Explanation:

    Using the relativistic Doppler shift formula which can be expressed as:

    \lambda_o = \lambda_s \sqrt{\dfrac{c+v}{c-v}}

    here;

    \lambda _o = wavelength measured in relative motion with regard to the source at velocity v

    \lambda_s = observed wavelength from the source’s frame.

    Given that:

    \lambda _o = 656.3 nm

    \lambda_s = 953.3 nm

    We will realize that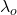 \lambda _o > \lambda_s; thus, v < 0 for this to be true.

    From the above equation, let’s make (v/c) the subject of the formula: we have:

    \dfrac{\lambda_o}{\lambda_s}=\sqrt{\dfrac{c+v}{c-v}}

    \Big(\dfrac{\lambda_o}{\lambda_s} \Big)^2=\dfrac{c+v}{c-v}

    \dfrac{v}{c} =\dfrac{\Big(\dfrac{\lambda_o}{\lambda_s} \Big)^2-1}{\Big(\dfrac{\lambda_o}{\lambda_s} \Big)^2+1}

    \dfrac{v}{c} =\dfrac{\Big(\dfrac{656.3}{953.3} \Big)^2-1}{\Big(\dfrac{656.3}{953.3} \Big)^2+1}

    \dfrac{v}{c} =0.357

    v = 0.357 c

    To m/s:

    1c = 299792458 m/s

    ∴

    0.357c = (299 792 458 × 0.357) m/s

    = 107025907.5 m/s

    = 1.07 × 10⁸ m/s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )