O rază de lumină cade sub un unghi de incidență i=30⁰ pe o suprafață plană ce separă două materiale transparente cu indici de re

Question

O rază de lumină cade sub un unghi de incidență i=30⁰ pe o suprafață

plană ce separă două materiale transparente cu indici de refracție n 1 = 1,60

și n 2 = 1,40.

Calculați unghiul de refracție (din mediul cu indicele de refracție mai mic).

Sugestie: sin 30⁰ = ½.

in progress 0
Cherry 3 years 2021-09-05T07:37:28+00:00 1 Answers 68 views 0

Answers ( )

  1. MichaelMet
    0
    2021-09-05T07:38:35+00:00
    Reply

    Answer:

    Explanation:

    The question in english is:

    A ray of light falls under an angle of incidence of 30 degrees on a flat surface that separates two transparent materials with indexes of refractions 1.60 and 1.40, respectively.

    Calculate the angle of refraction (from the environment with the lower index of refraction)

    Solution

    According to Snell’s Law :

    n_{1}sin(\theta_{1})=n_{2}sin(\theta_{2})

    Where:

    n_{1}=1.6  is the first medium index of refraction

    n_{2}=1.4  is the second medium index of refraction

    \theta_{1}=30\°  is the angle of the incident ray

    \theta_{2} is the angle of the refracted ray

    We need to find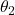 \theta_{2} from the equation above,

    \theta_{2}=sin^{-1}(\frac{n_{1}}{n_{2}}sin\theta_{1} )

    \theta_{2}=sin^{-1}(\frac{1.6}{1.4}sin(30\°)

    \theta_{2}=34.84\°

    Therefore, the angle of refraction is 34.84°

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )