If n is a positive integer, how many 5-tuples of integers from 1 through n can be formed in which the elements of the 5-tuple are written in

Question

If n is a positive integer, how many 5-tuples of integers from 1 through n can be formed in which the elements of the 5-tuple are written in increasing order but are not necessarily distinct? In other words, how many 5-tuples of integers (h, i, j, k, m) are there with 1 ≤ h ≤ i ≤ j ≤ k ≤ m ≤ n? As in Example 9.6.3, you can represent any ordered 5-tuple of integers (h, i, j, k, m) with 1 ≤ h ≤ i ≤ j ≤ k ≤ m ≤ n as a string of n − 1 vertical bars and 5 crosses, with the position of crosses indicating which 5 integers from 1 to n are included in the 5-tuple. Thus, the number of 5-tuples is the same as the number of strings of n+4 vertical bars and 5 crosses, which is n(n+1)(n+2)(n+3)(n+4) 120​ .

in progress 0
Huyền Thanh 3 years 2021-09-04T15:27:33+00:00 1 Answers 106 views 0

Answers ( )

  1. thienan
    0
    2021-09-04T15:29:26+00:00
    Reply

    Answer:

    \frac{(n+4)*(n+3)*(n+2)*(n+1)*n}{120}

    Step-by-step explanation:

    Given

    5 tuples implies that:

    n = 5

    (h,i,j,k,m) implies that:

    r = 5

    Required

    How many 5-tuples of integers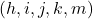 (h, i, j, k,m) are there such that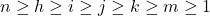n\ge h\ge i\ge j\ge k\ge m\ge 1

    From the question, the order of the integers h, i, j, k and m does not matter. This implies that, we make use of combination to solve this problem.

    Also considering that repetition is allowed:  This implies that, a number can be repeated in more than 1 location

    So, there are n + 4 items to make selection from

    The selection becomes:

    ^{n}C_r => ^{n + 4}C_5

    ^{n + 4}C_5 = \frac{(n+4)!}{(n+4-5)!5!}

    ^{n + 4}C_5 = \frac{(n+4)!}{(n-1)!5!}

    Expand the numerator

    ^{n + 4}C_5 = \frac{(n+4)!(n+3)*(n+2)*(n+1)*n*(n-1)!}{(n-1)!5!}

    ^{n + 4}C_5 = \frac{(n+4)*(n+3)*(n+2)*(n+1)*n}{5!}

    ^{n + 4}C_5 = \frac{(n+4)*(n+3)*(n+2)*(n+1)*n}{5*4*3*2*1}

    ^{n + 4}C_5 = \frac{(n+4)*(n+3)*(n+2)*(n+1)*n}{120}

    Solved

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )