If an object of 3.5 cm heitght is kept at a distance of 12 cm from the convex lens of focal length 8 cm. Find the position,nature and height

Question

If an object of 3.5 cm heitght is kept at a distance of 12 cm from the convex lens of focal length 8 cm. Find the position,nature and height of the height

in progress 0
Thiên Thanh 3 years 2021-08-14T04:53:08+00:00 1 Answers 8 views 0

Answers ( )

  1. diemkieu
    0
    2021-08-14T04:54:27+00:00
    Reply

    Answer: The image is at a distance of 24 cm on the right of the lens, it will be an inverted, real image and has a height of 7 cm.

    Explanation: To determine the position of the image of the object, use the Lens Equation, which is described by:

    \frac{1}{f} = \frac{1}{u} +\frac{1}{v}

    where

    f is focal length;

    u is distance of the object from the lens;

    v is distance of the image of the pbject from the lens;

    Calculating the position of the image will be:

    \frac{1}{v} =\frac{1}{f} - \frac{1}{u}

    \frac{1}{v} = \frac{1}{8} - \frac{1}{12}

    \frac{1}{v} = \frac{1}{24}

    v = 24 cm

    Note that the distance of the image from the lens is positive. This means that the formed image is positioned at the right of the lens and is inverted.

    For the height of the image, it can be used the Magnification (M) of an image:

    M =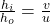 \frac{h_{i}}{h_{o}} = \frac{v}{u}

    where:

    h_{i} is the height of the image

    h_{o} is the height of the object

    For this image:

    \frac{h_{i}}{3.5} = \frac{24}{12}

    h_{i} = 2 * 3.5

    h_{i} = 7 cm

    The image formed for this lens is 24 cm on the right of the lens, inverted related to the object and has height of 7 cm.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )