Consider a block of mass m at rest on an inclined plane of angle theta. An acrobat of mass m_A is standing on the top corner of the block s

Question

Consider a block of mass m at rest on an inclined plane of angle theta. An acrobat of mass m_A is standing on the top corner of the block so that their weight presses vertically (perpendicular to the flat ground under the incline) downward. If the coefficient of static friction between the block and the incline is mu_s find an expression relating m_A, m, theta, and mu_s just before the block begins slipping. If the condition for slipping does not involve some of these parameters, leave them out.
Enter your expression as best you can and I will check it. Do not forget to upload your work as well.

in progress 0
Tài Đức 3 years 2021-08-16T22:26:59+00:00 1 Answers 5 views 0

Answers ( )

  1. minhkhoi
    0
    2021-08-16T22:28:17+00:00
    Reply

    Answer:

    μ = tan θ

    Explanation:

    For this exercise let’s use the translational equilibrium condition.

    Let’s set a datum with the x axis parallel to the plane and the y axis perpendicular to the plane.

    Let’s break down the weight of the block

             sin θ = Wₓ / W

             cos θ = W_y / W

             Wₓ = W sin θ

             W_y = W cos θ

    The acrobat is vertically so his weight decomposition is

             sin θ = = wₐₓ / wₐ

             cos θ = wₐ_y / wₐ

             wₐₓ = wₐ  sin θ

             wₐ_y = wₐ cos θ

    let’s write the equilibrium equations

    Y axis  

         N- W_y – wₐ_y = 0

         N = W cos θ + wₐ cos θ

    X axis

            Wₓ + wₐ_x – fr = 0

             fr = W sin θ + wₐ sin θ

    the friction force has the formula

             fr = μ N

             fr = μ (W cos θ + wₐ cos θ)

    we substitute

             μ (Mg cos θ + mg cos θ) = Mgsin θ + mg sin θ

             μ =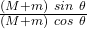 \frac{(M +m) \ sin \ \theta }{(M +m) \ cos \ \theta }

     

             μ = tan θ

    this is the minimum value of the coefficient of static friction for which the system is in equilibrium.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )