Share
Calculate the ratio of the kinetic energy of an electron to that of a proton if their wavelengths are equal. Assume that the speeds are nonr
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
the ratio of the kinetic energy of an electron to that of a proton if their wavelengths are equal is 1835.16 .
Explanation:
We know, wavelength is expressed in terms of Kinetic Energy by :
Therefore ,
It is given that both electron and proton have same wavelength.
Therefore,
Now, dividing equation 1 by 2 .
We get ,
Putting value of mass of electron =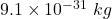 and mass of proton =
and mass of proton = 
We get :
Hence , this is the required solution.
Answer:
Explanation:
Given that the wavelengths of electron and proton are equal at non- relativistic speed.
From De-Broglie wave equation we know that:
where:
Then’
we’ve mass of electron,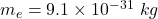
mass pf proton,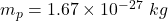
Now,
kinetic energy of electron:
kinetic energy of proton:
So,
from eq. (1)