At what temperature will uranium hexafluoride , the densest gas known have the same average speed as a molecule of the lightest gas, hydroge

Question

At what temperature will uranium hexafluoride , the densest gas known have the same average speed as a molecule of the lightest gas, hydrogen at 37 degree celcius

in progress 0
Sigridomena 3 years 2021-07-29T16:50:23+00:00 1 Answers 28 views 0

Answers ( )

  1. Gerda
    0
    2021-07-29T16:51:44+00:00
    Reply

    Answer:

    the required temperature of uranium hexafluoride is 54156.25 K

    Explanation:

    Given the data in the question;

    We know that average speed is;

    u = [ 3RT / MM ]^{1/2 ———– let this be equation 1

    where MM is the molar mass

    T is temperature

    R is universal gas constant and u is the average speed.

    First we get the average speed of H₂

    U_{H}₂ =  [ 3RT_H_2 / MM_H_2 ]^{1/2 —— let this be equation 2

    Next is the average speed of UF₆

    U_{UF₆ = [ 3RT_{UF_6} / MM_{UF_6} ]^{1/2 —— let this be equation 3

    given that; both have the same average speed, equation 2 = equation 3;

    [ 3RT_H_2 / MM_H_2 ]^{1/2 = [ 3RT_{UF_6} / MM_{UF_6} ]^{1/2

    we multiply both sides by 1/3R and also square both sides.

    [ T_H_2 / MM_H_2 ] = [ T_{UF_6} / MM_{UF_6} ]

    given that; temperature of hydrogen T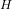_{H₂ = 37°C = ( 37 + 273.15)K = 310.15 K

    we know that Molar mass of H₂; MM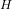_{H₂ = 2.016 g/mol  

    and molar mass of  UF₆; MM_{UF₆ = 352.02 g/mol

    so we substitute

    [ 310.15 K / 2.016 g/mol  ] = [ T_{UF₆ / 352.02 g/mol ]

    T_{UF₆ = [ 352.02 g/mol  × 310.15 K ] / 2.016 g/mol

    T_{UF₆ = 109179.003 K/ 2.016

    T_{UF₆ = 54156.25 K

    Therefore, the required temperature of uranium hexafluoride is 54156.25 K

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )