Share
Andrew plans to retire in 32 years. He plans to invest part of his retirement funds in stocks, so he seeks out information on past returns.
Question
Andrew plans to retire in 32 years. He plans to invest part of his retirement funds in stocks, so he seeks out information on past returns. He learns that over the entire 20th century, the real (that is, adjusted for inflation) annual returns on U.S. common stocks had mean 8.7% and standard deviation 20.2%. The distribution of annual returns on common stocks is roughly symmetric, so the mean return over even a moderate number of years is close to Normal.
(a) What is the probability (assuming that the past pattern of variation continues) that the mean annual return on common stocks over the next 40 years will exceed 13%?
(b) What is the probability that the mean return will be less than 8%?
in progress
0
Mathematics
3 years
2021-07-20T10:27:08+00:00
2021-07-20T10:27:08+00:00 1 Answers
62 views
0

Answers ( )
Answer:
a) 0.0885 = 8.85% probability that the mean annual return on common stocks over the next 40 years will exceed 13%.
b) 0.4129 = 41.29% probability that the mean return will be less than 8%
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean and standard deviation
and standard deviation  , the z-score of a measure X is given by:
, the z-score of a measure X is given by:
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean and standard deviation
and standard deviation  , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean  and standard deviation
and standard deviation  .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Mean 8.7% and standard deviation 20.2%.
This means that
40 years:
This means that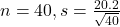
(a) What is the probability (assuming that the past pattern of variation continues) that the mean annual return on common stocks over the next 40 years will exceed 13%?
This is 1 subtracted by the pvalue of Z when X = 13. So
By the Central Limit Theorem
1 – 0.9115 = 0.0885
0.0885 = 8.85% probability that the mean annual return on common stocks over the next 40 years will exceed 13%.
(b) What is the probability that the mean return will be less than 8%?
This is the pvalue of Z when X = 8. So
0.4129 = 41.29% probability that the mean return will be less than 8%