Share
An electric motor drawing 10 amps at 110 V in steady state produces shaft power at 9.7 Nm and 1000 RPM. For a first Law analysis and conside
Question
An electric motor drawing 10 amps at 110 V in steady state produces shaft power at 9.7 Nm and 1000 RPM. For a first Law analysis and considering the motor as the control volume How much heat will be produced from the motor (in Watts)
in progress
0
Physics
3 years
2021-08-17T06:45:36+00:00
2021-08-17T06:45:36+00:00 1 Answers
10 views
0

Answers ( )
Answer:
The heat rate produced from the motor is 84.216 watts.
Explanation:
The electric motor receives power from electric current and releases power in the form of mechanical energy (torque) and waste heat and can be considered an stable-state system. The model based on the First Law of Thermodynamics for the electric motor is:
Where:
The heat transfer rate can be calculated in terms of electric and mechanic powers, that is:
The electric and mechanic powers are represented by the following expressions:
Where:
Now, the previous expression for heat transfer rate is expanded:
The angular speed, measured in radians per second, can be obtained by using the following expression:
Where:
If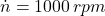 , then:
, then:
Given that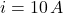 ,
, 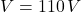 ,
, 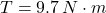 and
and 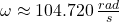 , the heat transfer rate from the electric motor is:
, the heat transfer rate from the electric motor is:
The heat rate produced from the motor is 84.216 watts.