A wheel of radius 0.5 m rotates with a constant angular speed about an axis perpendicular to its center. A point on the wheel that is 0.2 m

Question

A wheel of radius 0.5 m rotates with a constant angular speed about an axis perpendicular to its center. A point on the wheel that is 0.2 m from the center has a tangential speed of 2 m/s. Determine the tangential acceleration of the point that is 0.2 m from the center.

in progress 0
Khoii Minh 3 years 2021-08-06T19:12:33+00:00 1 Answers 131 views 0

Answers ( )

  1. Ladonna
    0
    2021-08-06T19:14:30+00:00
    Reply

    Answer:

    The tangential acceleration is 0 m/s².

    Explanation:

    Given:

    Radius of the wheel = 0.5 m

    The point of observation for calculating tangential acceleration = 0.2 m from center.

    Tangential speed at the point of observation = 2 m/s

    The angular speed of the wheel is a constant.

    In order to determine the tangential acceleration, we make use of the following formula:

    Tangential acceleration at a point = Angular acceleration × Distance of the point from center

    Or,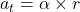 a_t=\alpha \times r

    Now, angular acceleration is defined as the rate of change of angular speed.

    Here, the angular speed of the wheel is a constant. So, the change of angular speed is 0. Therefore, the angular acceleration is also 0 rad/s².

    Now, from the above formula, as angular acceleration is 0, the magnitude of tangential acceleration at a point that is 0.2 m from the center of the wheel is also 0 m/s².

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )