Share
A train travels due north in a straight line with a constant speed of 100 m/s. Another train leaves a station 2,881 m away traveling on the
Question
A train travels due north in a straight line with a constant speed of 100 m/s. Another train leaves a station 2,881 m away traveling on the same track, but traveling due south with a constant speed of 136 m/s. At what position will the trains collide? Round to the nearest whole number.
in progress
0
Physics
3 years
2021-08-02T00:59:02+00:00
2021-08-02T00:59:02+00:00 1 Answers
16 views
0

Answers ( )
Answer:
The trains will collide at a distance 1660 m from the station
Explanation:
Let the train traveling due north with a constant speed of 100 m/s be Train A.
Let the train traveling due south with a constant speed of 136 m/s be Train B.
From the question, Train B leaves a station 2,881 m away (that is 2,881 m away from Train A position).
Hence, the two trains would have traveled a total distance of 2,881 m by the time they collide.
∴ If train A has covered a distance m by the time of collision, then train B would have traveled
m by the time of collision, then train B would have traveled 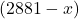 m.
m.
Also,
At the position where the trains will collide, the two trains must have traveled for equal time, t.
That is, At the point of collision,
From,
Since the time spent by the two trains is equal,
Then,
Hence,
This is the distance covered by train A by the time of collision.
Hence, Train B would have covered (2881 – 1221)m = 1660 m
Train B would have covered 1660 m by the time of collision
Since it is train B that leaves a station,
∴ The trains will collide at a distance 1660 m from the station.