Share
A thin rod of length 1.3 m and mass 88 g is suspended freely from one end. It is pulled to one side and then allowed to swing like a pendulu
Question
A thin rod of length 1.3 m and mass 88 g is suspended freely from one end. It is pulled to one side and then allowed to swing like a pendulum, passing through its lowest position with angular speed 2.39 rad/s. Neglecting friction and air resistance, find (a) the rod’s kinetic energy at its lowest position and (b) how far above that position the center of mass rises.
in progress
0
Physics
3 years
2021-08-12T11:25:46+00:00
2021-08-12T11:25:46+00:00 2 Answers
8 views
0

Answers ( )
Answer:
Explanation:
Given:
Length, L = 1.3 m
Mass, M = 88 g
= 0.088 kg
Angular velocity, w = 2.39 rad/s
Inertia of the rod = inertia of a cylinder = 1/12 M × L^2
Rotational inertia, I = Icm + I
= 1/12 M × L^2 + M × L/2
= 0.088 × (1/12 × 1.3^2 + 1.3/2)
= 0.088 × 0.79
= 0.05 kgm^2
Kinetic energy, E = 1/2 × l × w^2
= 1/2 × 0.05 × 2.39^2
= 0.142 J
B.
Using conservation of total mechanical energy,
Potential energy = kinetic energy
M × g × h = 0.142
h = 0.142/(9.8 × 0.088)
= 0.164 m
Answer:
a) the rod’s kinetic energy at its lowest position is 0.39 J
b) 0.459 m far above that position the center of mass rises.
Explanation:
Given
L = 1.3m
m = 88g
w = 2.39 rad/s
The rotational inertia of the road about an axis passing through its fixed end is given as follow
I = Icm + m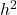
a)
The kinetic energy of the rod at the lowest point is given by the following
K =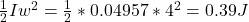
K is the kinetic energy of the rod at the lowest point
b)
From the conservation of the total mechanical energy of the rod
Ki + Ui = Kf + Uf
Ki = Uf – Ui + 0
mgh = K = 0.39
h = 0.39/mg = 0.39/0.088*9.8 = 0.459 m