A spherical wave with a wavelength of 2.0 mm is emitted from the origin. At one instant of time, the phase at rrr = 4.0 mm is πradπrad. At t

Question

A spherical wave with a wavelength of 2.0 mm is emitted from the origin. At one instant of time, the phase at rrr = 4.0 mm is πradπrad. At that instant, what is the phase at rrr_1 = 3.5 mm ? Express your answer to two significant figures and include the appropriate units.

in progress 0
King 3 years 2021-09-05T07:07:30+00:00 1 Answers 227 views 0

Answers ( )

  1. Philomena
    0
    2021-09-05T07:08:54+00:00
    Reply

    Complete Question

    A spherical wave with a wavelength of 2.0 mm is emitted from the origin. At one instant of time, the phase at r_1 = 4.0 mm is π rad. At that instant, what is the phase at r_2 = 3.5 mm ? Express your answer to two significant figures and include the appropriate units.

    Answer:

    The phase at the second point is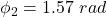  \phi _2 = 1.57 \ rad

    Explanation:

    From the question we are told that

        The wavelength of the spherical wave is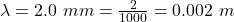  \lambda = 2.0 \ mm = \frac{2}{1000} = 0.002 \ m

        The first radius  is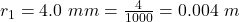  r_1 = 4.0 \ mm = \frac{4}{1000} = 0.004 \ m

         The phase at that instant is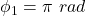  \phi _1 = \pi \ rad

         The second radius is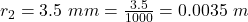  r_2 = 3.5 \ mm = \frac{3.5}{1000} = 0.0035 \ m

    Generally the phase difference is mathematically represented as

              \Delta \phi = \phi _2 - \phi _1

    this can also be expressed as

             \Delta \phi = \frac{2 \pi }{\lambda } (r_2 - r_1 )

    So we have that

       \phi _2 - \phi _1 = \frac{2 \pi }{\lambda } (r_2 - r_1 )

    substituting values

         \phi _2 - \pi = \frac{2 \pi }{0.002 } ( 0.0035 - 0.004 )

        \phi _2 = \frac{2 \pi }{0.002 } ( 0.0035 - 0.004 ) + 3.142

       \phi _2 = 1.57 \ rad

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )