A news report states that the 99% confidence interval for the mean number of daily calories consumed by participants in a medical study is (

Question

A news report states that the 99% confidence interval for the mean number of daily calories consumed by participants in a medical study is (1850, 2000). Assume the population distribution for daily calories consumed is normally distributed and that the confidence interval was based on a simple random sample of 18 observations. Calculate the sample mean, the margin of error, and the sample standard deviation based on the stated confidence interval and the given sample size. Use the t distribution in any calculations and round non-integer results to 4 decimal places.

in progress 0
Thạch Thảo 3 years 2021-07-23T13:30:03+00:00 1 Answers 5 views 0

Answers ( )

  1. giabao
    0
    2021-07-23T13:31:29+00:00
    Reply

    Answer:

    The sample mean is of 1925 calories.

    The margin of error is of 75 calories.

    The sample standard deviation is of 109.7992 calories.

    Step-by-step explanation:

    Sample mean:

    The sample mean is the mean value of the two bounds of the confidence interval. So

    M = \frac{1850 + 2000}{2} = 1925

    The sample mean is of 1925 calories.

    The margin of error

    Difference between the bounds and the sample mean. So

    2000 – 1925 = 1925 – 1850 = 75 calories.

    The margin of error is of 75 calories.

    Sample standard deviation:

    Here, I am going to expand on the t-distribution.

    The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So

    df = 18 – 1 = 17

    99% confidence interval

    Now, we have to find a value of T, which is found looking at the t table, with 17 degrees of freedom(y-axis) and a confidence level of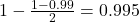 1 - \frac{1 - 0.99}{2} = 0.995. So we have T = 2.898

    The margin of error is:

    M = T\frac{s}{\sqrt{n}}

    In which s is the standard deviation of the sample and n is the size of the sample.

    Since M = 75, T = 2.898, n = 18

    M = T\frac{s}{\sqrt{n}}

    75 = 2.898\frac{s}{\sqrt{18}}

    s = \frac{75\sqrt{18}}{2.898}

    s = 109.7992

    The sample standard deviation is of 109.7992 calories.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )