A line passes through the points (-1, -1) and (5,8). Which points lie on the same line? Select all that apply. (-3, -4)

Question

A line passes through the points (-1, -1)
and (5,8). Which points lie on the same
line? Select all that apply.
(-3, -4)
(9, 14)
(1, 2)
(4, 7)
(3,5)
(-2,-2)

in progress 0
Orla Orla 3 years 2021-07-26T16:46:26+00:00 1 Answers 181 views -1

Answers ( )

  1. Jezebel
    0
    2021-07-26T16:47:29+00:00
    Reply

    Given:

    A line passes through the points (-1, -1) and (5,8).

    To find:

    Which points lie on the same line?

    Solution:

    If a line passes through two points, then the equation of the line is:

    y-y_1=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)

    A line passes through the points (-1, -1) and (5,8). So, the equation of the line is:

    y-(-1)=\dfrac{8-(-1)}{5-(-1)}(x-(-1))

    y+1=\dfrac{8+1}{5+1}(x+1)

    y+1=\dfrac{9}{6}(x+1)

    y+1=\dfrac{3}{2}(x+1)

    Multiply both sides by 2.

    2(y+1)=3(x+1)

    2y+2=3x+3

    2y=3x+3-2

    y=\dfrac{3}{2}x+\dfrac{1}{2}

    So, the equation of the line is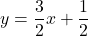 y=\dfrac{3}{2}x+\dfrac{1}{2}.

    Now, check each point for this equation.

    Putting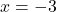 x=-3, we get

    y=\dfrac{3}{2}(-3)+\dfrac{1}{2}

    y=\dfrac{-9+1}{2}

    y=\dfrac{-8}{2}

    y=-4

    Similarly,

    For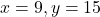 x=9,y=15.

    For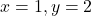 x=1,y=2.

    For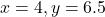 x=4,y=6.5.

    For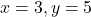 x=3,y=5.

    For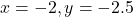 x=-2,y=-2.5.

    Therefore, the points (-3,-4), (9,14), (1,2) and (3,5) lie on the same line but the points (4,7) and (-2,-2) are not on that line.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )