A curve of radius 151 m is banked at an angle of 11°. An 838-kg car negotiates the curve at 86 km/h without skidding. Neglect the effects of

Question

A curve of radius 151 m is banked at an angle of 11°. An 838-kg car negotiates the curve at 86 km/h without skidding. Neglect the effects of air drag and rolling friction. Find the following.
(a) the normal force exerted by the pavement on the tires
kN ?

(b) the frictional force exerted by the pavement on the tires
kN ?

(c) the minimum coefficient of static friction between the pavement and the tires?

in progress 0
Ngọc Khuê 3 years 2021-08-23T04:50:25+00:00 1 Answers 3 views 0

Answers ( )

  1. thienan
    0
    2021-08-23T04:51:45+00:00
    Reply

    a) 8.52 kN

    b) 0.74 kN

    c) 0.087

    Explanation:

    a)

    There are 3 forces acting on the car on the banked curve:

    – The weight of the car, mg, vertically downward

    – The normal force of the pavement on the tires, N, upward perpendicular to the road

    – The force of friction,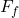 F_f, down along the road

    Resolving the 3 forces along two perpendicular directions (horizontal and vertical), we obtain the equations of motions:

    x- direction:

    N sin \theta +F_f cos \theta = m \frac{v^2}{r} (1)

    y- direction:

    Ncos \theta -F_f sin \theta-mg =0 (2)

    where

    \theta=11^{\circ} is the angle of the ramp

    F_f is the force of friction

    m = 838 kg is the mass of the car

    r = 151 m is the radius of the curve

    v=86 km/h =23.9 m/s is the speed of the car

    Solving eq.(2) for Ff and substituting into eq.(1), we can find the normal force:

    From (2):

    F_f=\frac{Ncos \theta-mg}{sin \theta} (3)

    Substituting into (1) and re-arranging,

    N sin \theta +\frac{N cos \theta -mg}{sin \theta} cos \theta = m \frac{v^2}{r}\\N(sin \theta+\frac{cos^2 \theta}{sin \theta})=m\frac{v^2}{r}+mg\frac{cos \theta}{sin \theta}\\N=\frac{\frac{mv^2}{r}+mg \frac{cos \theta}{sin \theta}}{sin \theta + \frac{cos^2\theta}{sin \theta}}=8518.3 N = 8.52 kN

    b)

    The frictional force between the pavement and the tires,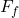 F_f, can be found by using eq.(3) derived in part a):

    F_f=\frac{Ncos \theta-mg}{sin \theta}

    where we have:

    N=8518.3 N is the normal force

    \theta=11^{\circ} is the angle of the ramp

    m = 838 kg is the mass of the car

    g=9.81 m/s^2 is the acceleration due to gravity

    Substituting the values, we find:

    F_f=\frac{(8518.3)cos 11^{\circ}-(838)(9.81)}{sin 11^{\circ}}=739.0 N = 0.74 kN

    c)

    The force of friction between the road and the tires can be rewritten as

    F_f=\mu_s N

    where

    \mu_s is the coefficient of static friction

    N is the normal force exerted by the road on the car

    In this problem, we know that

    N = 8.52 kN is the normal force

    F_f=0.74 kN is the frictional force

    Therefore, the minimum coefficient of static friction between the pavement and the tires is:

    \mu_s = \frac{F_f}{N}=\frac{0.74}{8.52}=0.087

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )