A coil is formed by winding 190 turns of insulated 16 gauge copper wire (diameter = 1.9 mm) in a single layer on a cylindrical form of radiu

Question

A coil is formed by winding 190 turns of insulated 16 gauge copper wire (diameter = 1.9 mm) in a single layer on a cylindrical form of radius 9.2 cm. What is the resistance of the coil? Neglect the thickness of the insulation. (Take the resistivity of copper to be 1.69 × 10-8 ohm-m.)

in progress 0
Delwyn 3 years 2021-09-05T03:27:02+00:00 2 Answers 4 views 0

Answers ( )

  1. MichaelMet
    0
    2021-09-05T03:28:07+00:00
    Reply

    Answer:

    The resistance of the coil is 0.655 Ω

    Explanation:

    Given that,

    Number of turns = 190 turns

    Diameter of coil= 1.9 mm = 0.95 mm

    Radius of single layer = 9.2 cm

    Pressure = 16 gauge

    We need to calculate the length of the wire

    Using formula of length

    L=n2\pi r

    Where, n = number of turns

    r = radius of cylinder

    Put the value into the formula

    L=190\times2\pi\times9.2\times10^{-2}

    L=109.8\ m

    We need to calculate the area of cross section

    Using formula of area

    A=\pi\times r^2

    Put the value into the formula

    A=\pi\times(0.95\times10^{-3})^2

    A=0.000002835\ m^2

    A=2.83\times10^{-6}\ m^2

    We need to calculate the resistance of the coil

    Using formula of resistivity

    R=\dfrac{\rho\times l}{A}

    Put the value into the formula

    R=\dfrac{1.69\times10^{-8}\times109.8}{2.83\times10^{-6}}

    R=0.655\ \Omega

    Hence, The resistance of the coil is 0.655 Ω

  2. Vodka
    0
    2021-09-05T03:28:36+00:00
    Reply

    Explanation:

    The given data is as follows.

    number of turns = n = 190 turns

    radius = r = 9.2 cm = 0.092 m

    diameter of copper wire = d = 1.9 mm

    radius of copper wire = r_{c} = \frac{d}{2}

                         = \frac{1.9}{2}    

                         = 0.95 \times 10^{-3} m

    where,  A = cross sectional area of the wire

    As, length of each turn of wire is 2pr where r is radius of the coil.

      L = 190(2pr)

         = 190 \times 6.28 \times 0.092 m

          = 109.77 m

    The cross sectional area of the wire is as follows.

           A =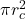 \pi r^{2}_{c}

               = 3.14 (0.95 \times 10^{-3} m)^{2}

              = 2.83 \times 10^{-6} m^{2}

    It is given that resistivity of copper wire is 1.69 \times 10^{-8} \ohm

                  R = \rho \frac{L}{A}

                      = 1.69 \times 10^{-8} \ohm \times \frac{109.77}{2.83 \times 10^{-6} m^{2}}

                     = 65.53 \times 10^{-2} \ohm

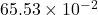
    Thus, we can conclude that resistance of the coil is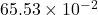 65.53 \times 10^{-2} \ohm.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )