A beam of alpha particles ( q = +2e, mass = 6.64 x 10-27 kg) is accelerated from rest through a potential difference of 1.8 kV. The beam is

Question

A beam of alpha particles ( q = +2e, mass = 6.64 x 10-27 kg) is accelerated from rest through a potential difference of 1.8 kV. The beam is then entered into a region between two parallel metal plates with potential difference 120 V and a separation 8 mm, perpendicular to the direction of the field. What magnitude of magnetic field is needed so that the alpha particles emerge undeflected from between the plates?

in progress 0
Thạch Thảo 3 years 2021-07-20T10:47:38+00:00 1 Answers 30 views 0

Answers ( )

  1. mocmien2
    0
    2021-07-20T10:48:44+00:00
    Reply

    Answer:

    The magnetic field required required for the beam not to be deflected  is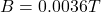 B = 0.0036T

    Explanation:

    From the question we are told that

        The charge on the particle is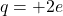 q = +2e

        The mass of the particle is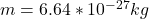  m = 6.64 *10^{-27} kg

        The potential difference is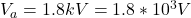 V_a = 1.8 kV = 1.8 *10^{3} V

        The potential difference between the two parallel plate is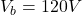  V_b = 120 V

        The separation between the plate is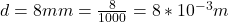  d = 8 mm = \frac{8}{1000} = 8*10^{-3}m

       

    The Kinetic energy experienced by the beam before entering the region of the parallel plate is equivalent to the potential energy of the beam  after the region having a potential difference of 1.8kV

                   KE_b = PE_b

    Generelly

                  KE_b = \frac{1}{2} m v^2

    And      PE_b = q V_a

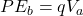
     Equating this two formulas

                  \frac{1}{2} mv^2 = q V_a

    making v the subject

               v = \sqrt{\frac{q V_a}{2 m} }

    Substituting value  

               v = \sqrt{\frac{ 2* 1.602 *10^{-19} * 1.8 *10^{3}}{2 * 6.64 *10^{-27}} }

               v = 41.65*10^4 m/s

    Generally the electric field between the plates is mathematically represented as

                     E = \frac{V_b}{d}  

    Substituting value  

                     E = \frac{120}{8*10^{-3}}              

                    E = 15 *10^3 NC^{-1}

    the magnetic field  is mathematically evaluate    

                         B = \frac{E}{v}

                       B = \frac{15 *10^{3}}{41.65 *10^4}

                        B = 0.0036T

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )