A 3200-lb car is moving at 64 ft/s down a 30-degree grade when it runs out of fuel. Find its velocity after that if friction exerts a resist

Question

A 3200-lb car is moving at 64 ft/s down a 30-degree grade when it runs out of fuel. Find its velocity after that if friction exerts a resistive force with magnitude proportional to the square of the speed with k

in progress 0
Diễm Thu 3 years 2021-08-09T15:28:48+00:00 1 Answers 16 views 0

Answers ( )

  1. danthu
    0
    2021-08-09T15:30:24+00:00
    Reply

    Answer:

    The velocity is 40 ft/sec.

    Explanation:

    Given that,

    Force = 3200 lb

    Angle = 30°

    Speed = 64 ft/s

    The resistive force with magnitude proportional to the square of the speed,

    F_{r}=kv^2

    Where, k = 1 lb s²/ft²

    We need to calculate the velocity

    Using balance equation

    F\sin\theta-F_{r}=m\dfrac{d^2v}{dt^2}

    Put the value into the formula

    3200\sin 30-kv^2=m\dfrac{d^2v}{dt^2}

    Put the value of k

    3200\times\dfrac{1}{2}-v^2=m\dfrac{d^2v}{dt^2}

    1600-v^2=m\dfrac{d^2v}{dt^2}

    At terminal velocity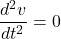 \dfrac{d^2v}{dt^2}=0

    So,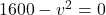 1600-v^2=0

    v=\sqrt{1600}

    v=40\ ft/sec

    Hence, The velocity is 40 ft/sec.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )