A 2.0-mm-long, 1.0-mmmm-diameter wire has a variable resistivity given by rho(x)=(2.5×10−6)[1+(x1.0m)2]Ωmrho(x)=(2.5×10−6)[1+(x1.0m)2]Ωm whe

Question

A 2.0-mm-long, 1.0-mmmm-diameter wire has a variable resistivity given by rho(x)=(2.5×10−6)[1+(x1.0m)2]Ωmrho(x)=(2.5×10−6)[1+(x1.0m)2]Ωm where xx is measured from one end of the wire.What is the current if this wire is connected to the terminals of a 17.0V battery?

in progress 0
Thiên Hương 3 years 2021-07-25T12:59:44+00:00 1 Answers 43 views 0

Answers ( )

  1. linhdan
    0
    2021-07-25T13:01:02+00:00
    Reply

    Answer:

    1.144 A

    Explanation:

    given that;

    the length of the wire = 2.0 mm

    the diameter of the wire = 1.0 mm

    the variable resistivity R = \rho (x) =(2.5*10^{-6})[1+(\frac{x}{1.0 \ m})^2]

    Voltage of the battery = 17.0 v

    Now; the resistivity of the variable (dR) can be expressed as =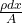 \frac{\rho dx}{A}

    dR = \frac{(2.5*10^{-6})[1+(\frac{x}{1.0})^2]}{\frac{\pi}{4}(10^{-3})^2}

    Taking the integral of both sides;we have:

    \int\limits^R_0 dR = \int\limits^2_0 3.185 \ [1+x^2] \ dx

    R = 3.185 [x + \frac {x^3}{3}}]^2__0

    R = 3.185 [2 + \frac {2^3}{3}}]

    R = 14.863 Ω

    Since V = IR

    I = \frac{V}{R}

    I = \frac{17}{14.863}

    I = 1.144 A

    ∴  the current if this wire if it is connected to the terminals of a 17.0V battery = 1.144 A

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )