Share
1) Steven carefully places a 1.85 kg wooden block on a frictionless ramp, so that the block begins to slide down the ramp from rest. The ram
Question
1) Steven carefully places a 1.85 kg wooden block on a frictionless ramp, so that the block begins to slide down the ramp from rest. The ramp makes an angle of 59.3° up from the horizontal. Which forces below do non-zero work on the block as it slides down the ramp?a) gravityb) normalc) frictiond) spring2) How much total work has been done on the block after it slides down along the ramp a distance of 1.85 m? 3) Nancy measures the speed of the wooden block after it has gone the 1.85 m down the ramp. Predict what speed she should measure.4) Now, Steven again places the wooden block back at the top of the ramp, but this time he jokingly gives the block a big push before it slides down the ramp. If the block’s initial speed is 2.00 m / s and the block again slides down the ramp 1.91 m , what should Nancy measure for the speed of the block this time?
in progress
0
Physics
3 years
2021-09-03T10:33:34+00:00
2021-09-03T10:33:34+00:00 1 Answers
0 views
0

Answers ( )
1) a) Gravity
2) 28.8 J
3) 5.6 m/s
4) 6.0 m/s
Explanation:
1)
When the block is sliding down along the ramp, we have only two forces acting on it:
– The force of gravity, whose direction is always vertically downward
– The normal reaction of the plane on the block, which is perpendicular to the ramp itself
The work done by a force on an object is given by:
where F is the magnitude of the force, d is the displacement of the object, the angle between the direction of the force and of the displacement
the angle between the direction of the force and of the displacement
From the equation, we observe that:
– The force of gravity acts at an angle of with respect to the direction of motion of the block, so the work done by gravity is non-zero
with respect to the direction of motion of the block, so the work done by gravity is non-zero
– The normal reaction, however, is perpendicular to the direction of motion of the block, so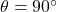 ; this means that
; this means that 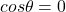 , so the normal reaction does no work on the block.
, so the normal reaction does no work on the block.
Therefore, the only force that does non-zero work is
a) gravity
2)
The total work done on the block as it slides down is just the net work done by gravity (because the normal force does no work), so it is given by:
where:
m = 1.85 kg is the mass of the block
d = 1.85 m is the displacement of the block
Substituting into the equation, we find the work done:
3)
In order to find the speed of the block after covering 1.85 m, we can use the work-energy theorem, which states that the work done on an object is equal to its change in kinetic energy:
where:
m = 1.85 kg is the mass of the block
u = 0 is the initial speed of the block (it starts from rest)
v is the final speed of the block
Solving for v, we can find the final speed of the block, that is:
4)
In this case:
– The displacement of the block is d = 1.91 m
Therefore, the work done on the block by gravity is:
– The initial speed of the block is u = 2.00 m/s
So, the equation of the work-energy theorem becomes
And since the mass of the block is
m = 1.85 kg
Solving for v, we find new final speed of the block: