In 1980, the median age of the U.S. population was 30.0; in 2000, the median age was 35.3. Consider 1980 as the starting point (time zero) f

Question

In 1980, the median age of the U.S. population was 30.0; in 2000, the median age was 35.3. Consider 1980 as the starting point (time zero) for this problem. Create an explicit exponential formula for the median age of the U.S. population t years after 1980, assuming the median age has exponential growth.

in progress 0
Philomena 3 years 2021-07-30T01:30:03+00:00 1 Answers 23 views 0

Answers ( )

  1. Ladonna
    0
    2021-07-30T01:31:17+00:00
    Reply

    Answer: 30e^{0.00813x}

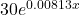
    Step-by-step explanation:

    Given

    Median age in 1980 is 30

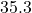    It is 35.3 in year 2000

    Suppose the median age follows the function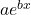 ae^{bx}. Consider 1980 as starting year. Write the equation for year 1980

    \Rightarrow 30=ae^{b(0)}\\\Rightarrow 30=a

    For year 2000

    \Rightarrow 35.3=30e^{20b}\\\\\Rightarrow \dfrac{30e^{20b}}{30}=\dfrac{35.3}{30}\\\\\Rightarrow e^{20b}=1.17666\\\\\Rightarrow b=0.00813

    After t years of 1980

    \Rightarrow 30e^{0.00813x}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )