Share
If f(a) is an exponential function where f(-3) = 18 and f(1) = 59, then find the value of f(0), to the nearest hundredth.
Question
If f(a) is an exponential function where f(-3) = 18 and f(1) = 59, then find the
value of f(0), to the nearest hundredth.
in progress
0
Mathematics
3 years
2021-07-31T15:31:13+00:00
2021-07-31T15:31:13+00:00 1 Answers
6 views
0

Answers ( )
Given:
For en exponential function f(a):
To find:
The value of f(0).
Solution:
The general form of an exponential function is:
Where, a is the initial value and b is the growth/ decay factor.
We have,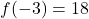 . Substitute
. Substitute  in (i).
in (i).
We have,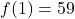 . Substitute
. Substitute 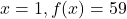 in (i).
in (i).
On dividing (iii) by (ii), we get
Substituting the value of b in (iii).
The initial value of the function is 43.83. It means, .
.
Therefore, the value of f(0) is 43.83.