Find the minimum uncertainty in the speed of a bacterium having mass 3.0 × 10−15 kg if we know the position of the bacterium to within its l

Question

Find the minimum uncertainty in the speed of a bacterium having mass 3.0 × 10−15 kg if we know the position of the bacterium to within its length of 1.0 µm

in progress 0
Latifah 3 years 2021-09-05T13:25:42+00:00 1 Answers 37 views 0

Answers ( )

  1. thuthuy
    0
    2021-09-05T13:26:56+00:00
    Reply

    Answer:

    The minimum uncertainty in the speed of a bacterium is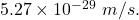 5.27\times 10^{-29}\ m/s.

    Explanation:

    We know by Heisenberg Uncertainty principal :

    \Delta p\times \Delta x=\dfrac{h}{4\pi}\\\\m\Delta v\times \Delta x=\dfrac{h}{4\pi}\\\\\Delta v\times \Delta x=\dfrac{h}{4\pi m}  ….equation 1.

    Putting value of \Delta x, m ,h in above equation we get :

    \Delta v\times 10^{-6}\ m=\dfrac{6.626\times 10^{-34}}{4\times \dfrac{22}{7}}\\\\\Delta v=\dfrac{6.626\times 10^{-34}}{4\times \dfrac{22}{7}\times 10^{-6}}=5.27\times 10^{-29}\ m/s.

    Hence, this is the required solution.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )