An ideal monatomic gas initially has a temperature of T and a pressure of p. It is to expand from volume V1 to volume V2. If the expansion i

Question

An ideal monatomic gas initially has a temperature of T and a pressure of p. It is to expand from volume V1 to volume V2. If the expansion is isothermal, what are the final pressure pfi and the work Wi done by the gas? If, instead, the expansion is adiabatic, what are the final pressure pfa and the work Wa done by the gas? State your answers in terms of the given variables.

in progress 0
Bơ 3 years 2021-07-15T16:58:53+00:00 1 Answers 4 views 0

Answers ( )

  1. dangkhoa
    0
    2021-07-15T17:00:43+00:00
    Reply

    Answer:

    Isothermal :   P2 = ( P1V1 / V2 ) ,  work-done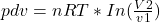 pdv = nRT * In( \frac{V2}{v1} )

    Adiabatic : : P2 =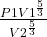 \frac{P1V1^{\frac{5}{3} } }{V2^{\frac{5}{3} } }  , work-done =

    W =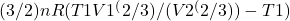 (3/2)nR(T1V1^(2/3)/(V2^(2/3)) - T1)

    Explanation:

    initial temperature : T

    Pressure : P

    initial volume : V1

    Final volume : V2

    A) If expansion was isothermal calculate final pressure and work-done

    we use the gas laws

    = PIVI = P2V2

    Hence : P2 = ( P1V1 / V2 )

    work-done :

    pdv = nRT * In( \frac{V2}{v1} )

    B) If the expansion was Adiabatic show the Final pressure and work-done

    final pressure

    P1V1^y = P2V2^y

    where y = 5/3

    hence : P2 =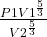 \frac{P1V1^{\frac{5}{3} } }{V2^{\frac{5}{3} } }

    Work-done

    W =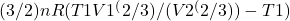 (3/2)nR(T1V1^(2/3)/(V2^(2/3)) - T1)

    Where    T2 = T1V1^(2/3)/V2^(2/3)

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )