A rectangular tank 60 cm long and 50 cm wide is /5 full of water. When 24 liters of water are added, the water level rises to the brim of th

Question

A rectangular tank 60 cm long and 50 cm wide is /5 full of water. When 24 liters of water are added, the water level rises to the brim of the tank. Find the height of the tank. (1 liter is 1000cm3 )

in progress 0
Adela 3 years 2021-07-31T03:56:02+00:00 1 Answers 29 views 0

Answers ( )

  1. thanhha
    0
    2021-07-31T03:57:34+00:00
    Reply

    Answer:

    The tank is 10cm high

    Step-by-step explanation:

    Given

    L=60cm — length

    W=60cm — width

    x = \frac{1}{5} — water lever

    Addition = 24L

    Required

    The height of the tank

    Let y represents the remaining fraction before water is added.

    So:

    y + x = 1

    Make y the subject

    y = 1 - x

    y = 1 - \frac{1}{5}

    Solve

    y = \frac{5 - 1}{5}

    y = \frac{4}{5}

    Represent the volume of the tank with v

    So:

    y * v = 24L

    Make v the subject

    v = \frac{24L}{y}

    Substitute: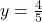 y = \frac{4}{5}

    v = \frac{24L}{4/5}

    v = 30L

    Represent the height of the tank with h;

    So, the volume of the tank is:

    v = lwh

    Make h the subject

    h = \frac{v}{lw}

    Substitute values for v, l and w

    h = \frac{30L}{60cm * 50cm}

    Convert 30L to cm^3

    h = \frac{30*1000cm^3}{60cm * 50cm}

    h = \frac{30000cm^3}{3000cm^2}

    h = 10cm

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )