A helicopter is ascending vertically with a speed of 5.32 m/s . At a height of 120 m above the Earth, a package is dropped from the helicopt

Question

A helicopter is ascending vertically with a speed of 5.32 m/s . At a height of 120 m above the Earth, a package is dropped from the helicopter.
How much time does it take for the package to reach the ground? [Hint: What is v0 for the package?]

in progress 0
Thiên Thanh 3 years 2021-07-18T13:18:11+00:00 1 Answers 9 views 0

Answers ( )

  1. thucuc
    0
    2021-07-18T13:19:23+00:00
    Reply

    Answer:

    Approximately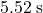 5.52\; \rm s (assuming that g = -9.81\; \rm m\cdot s^{-2}.)

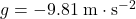    Explanation:

    From the perspective of an observer on the ground, the package was initially moving with the helicopter. The initial velocity of that package (v_0) would be the same as the velocity of the helicopter. In other words, v_0 = 5.32\; \rm m \cdot s^{-1}.

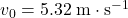    Other quantities:

    • a = g \approx -9.81\; \rm m \cdot s^{-2}. (The g here is negative because the acceleration due to gravity points downwards.)
    • x = -120\; \rm m \cdot s^{-1} (The position of the package would have changed by 120\; \rm m by the time it reached the ground. The negative sign is because this position change also points downwards.)

    There are two ways to find the time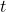 t required for the package to reach the ground after it was dropped.

    The first approach makes use of the SUVAT equation:

    \displaystyle x = \frac{1}{2}\, a\, t^2 - v_0\, t.

    For this question, x, a, and v_0 are already known. However, this approach would require solving a quadratic equation where the coefficient for the first-order term is non-zero.

    An alternative approach is to solve for v_1, the velocity of the package right before it reaches the ground. From the SUVAT equation that does involve time:

    \displaystyle {v_1}^{2} - {v_0}^{2} = 2\, a\, x.

    Again, x, a, and v_0 are already known. Solve for v_1:

    \begin{aligned}v_1 &= \sqrt{2\, a\, x + {v_0}^2} \\ &\approx \sqrt{2\times (-9.81) \times (-120) + 5.32^2} \approx -48.81293\; \rm m \cdot s^{-1}\end{aligned}.

    Calculate time from the change in velocity:

    \displaystyle t = \frac{v_1 - v_0}{a} \approx 5.52\; \rm s.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )