A fancart of mass 0.8 kg initially has a velocity of < 0.8, 0, 0 > m/s. Then the fan is turned on, and the air exerts a constant force

Question

A fancart of mass 0.8 kg initially has a velocity of < 0.8, 0, 0 > m/s. Then the fan is turned on, and the air exerts a constant force of < −0.4, 0, 0 > N on the cart for 1.5 seconds. What is the change in kinetic energy of the fancart over this 1.5 second interval?

in progress 0
Thu Hương 3 years 2021-08-13T17:35:04+00:00 1 Answers 362 views 0

Answers ( )

  1. minhkhang
    0
    2021-08-13T17:36:31+00:00
    Reply

    Answer:

    The change in kinetic energy of the fancart over 1.5 second time interval is -0.255 J

    Explanation:

    Given;

    mass of fancart, m = 0.8 kg

    initial velocity of fancart, u = < 0.8, 0, 0 > m/s

    force exerted by air on fancart, F = < −0.4, 0, 0 > N

    duration of the force, t =  1.5 seconds

    The change in kinetic energy of the fancart over 1.5 second time interval;

    Determine the final velocity, v

    F = ma

    a = F/m

    Apply equation of motion;

    v = u + at

    v = u + \frac{F}{m}t

    v = 0.8 + \frac{-0.4*1.5}{0.8}\\\\v = 0.8 -0.75\\\\v = 0.05\ m/s

    Change in Kinetic energy = final kinetic energy – initial kinetic energy

    ΔKE = KE (final) – KE(initial)

    ΔKE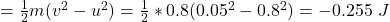 = \frac{1}{2} m(v^2-u^2) = \frac{1}{2}* 0.8(0.05^2-0.8^2) = -0.255 \ J

    Therefore, the change in kinetic energy of the fancart over 1.5 second time interval is -0.255 J

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )