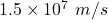A constant electric field with magnitude 1.50 ✕ 103 N/C is pointing in the positive x-direction. An electron is fired from x = −0.0200 m i

Question

A constant electric field with magnitude 1.50 ✕ 103 N/C is pointing in the positive x-direction. An electron is fired from x = −0.0200 m in the same direction as the electric field. The electron’s speed has fallen by half when it reaches x = 0.190 m, a change in potential energy of 5.04 ✕ 10−17 J. The electron continues to x = −0.210 m within the constant electric field. If there’s a change in potential energy of −9.60 ✕ 10−17 J as it goes from x = 0.190 m to x = −0.210 m, find the electron’s speed (in m/s) at x = −0.210 m.

in progress 0
Diễm Thu 3 years 2021-07-15T20:07:55+00:00 1 Answers 23 views 0

Answers ( )

  1. Tryphena
    0
    2021-07-15T20:09:35+00:00
    Reply

    Answer:

    The speed of electron is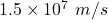 1.5\times10^{7}\ m/s

    Explanation:

    Given that,

    Electric field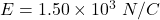 E=1.50\times10^{3}\ N/C

    Distance = -0.0200

    The electron’s speed has fallen by half when it reaches x = 0.190 m.

    Potential energy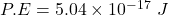 P.E=5.04\times10^{-17}\ J

    Change in potential energy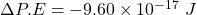 \Delta P.E=-9.60\times10^{-17}\ J as it goes x = 0.190 m to x = -0.210 m

    We need to calculate the work done by the electric field

    Using formula of work done

    W=-eE\Delta x

    Put the value into the formula

    W=-1.6\times10^{-19}\times1.50\times10^{3}\times(0.190-(-0.0200))

    W=-5.04\times10^{-17}\ J

    We need to calculate the initial velocity

    Using change in kinetic energy,

    \Delta K.E = \dfrac{1}{2}m(\dfrac{v}{2})^2+\dfrac{1}{2}mv^2

    \Delta K.E=\dfrac{-3mv^2}{8}

    Now, using work energy theorem

    \Delta K.E=W

    \Delta K.E=\Delta U

    So, \Delta U=W

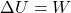
    Put the value in the equation

    \dfrac{-3mv^2}{8}=-5.04\times10^{-17}

    v^2=\dfrac{8\times(5.04\times10^{-17})}{3m}

    Put the value of m

    v=\sqrt{\dfrac{8\times(5.04\times10^{-17})}{3\times9.1\times10^{-31}}}

    v=1.21\times10^{7}\ m/s

    We need to calculate the change in potential energy

    Using given potential energy

    \Delta U=-9.60\times10^{-17}-(-5.04\times10^{-17})

    \Delta U=-4.56\times10^{-17}\ J

    We need to calculate the speed of electron

    Using change in energy

    \Delta U=-W=-\Delta K.E

    \Delta K.E=\Delta U

    \dfrac{1}{2}m(v_{f}^2-v_{i}^2)=4.56\times10^{-17}

    Put the value into the formula

    v_{f}=\sqrt{\dfrac{2\times4.56\times10^{-17}}{9.1\times10^{-31}}+(1.21\times10^{7})^2}

    v_{f}=1.5\times10^{7}\ m/s

    Hence, The speed of electron is 1.5\times10^{7}\ m/s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )