A closed, rectangular-faced box with a square base is to be constructed using only 36 m2 of material. What should the height h and base leng

Question

A closed, rectangular-faced box with a square base is to be constructed using only 36 m2 of material. What should the height h and base length b of the box be so as to maximize its volume

in progress 0
Trung Dũng 3 years 2021-08-03T16:49:39+00:00 1 Answers 83 views 0

Answers ( )

  1. thnahdat
    0
    2021-08-03T16:50:41+00:00
    Reply

    Answer:

    b=h=\sqrt{6} m

    Step-by-step explanation:

    Let

    Bas length of box=b

    Height of box=h

    Material used in constructing of box=36 square m

    We have to find the height h and base length b of the box to maximize the volume of box.

    Surface area of box=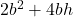2b^2+4bh

    2b^2+4bh=36

    b^2+2bh=18

    2bh=18-b^2

    h=\frac{18-b^2}{2b}

    Volume of box, V=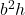b^2h

    Substitute the values

    V=b^2\times \frac{18-b^2}{2b}

    V=\frac{1}{2}(18b-b^3)

    Differentiate w. r.t b

    \frac{dV}{db}=\frac{1}{2}(18-3b^2)

    \frac{dV}{db}=0

    \frac{1}{2}(18-3b^2)=0

    \implies 18-3b^2=0

    \implies 3b^2=18

    b^2=6

    b=\pm \sqrt{6}

    b=\sqrt{6}

    The negative value of b is not possible because length cannot be negative.

    Again differentiate w.r.t b

    \frac{d^2V}{db^2}=-3b

    At  b=\sqrt{6}

    \frac{d^2V}{db^2}=-3\sqrt{6}<0

    Hence, the volume of box is maximum at b=\sqrt{6}.

    h=\frac{18-(\sqrt{6})^2}{2\sqrt{6}}

    h=\frac{18-6}{2\sqrt{6}}

    h=\frac{12}{2\sqrt{6}}

    h=\sqrt{6}

    b=h=\sqrt{6} m

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )