You measure 20 turtles’ weights, and find they have a mean weight of 45 ounces. Assume the population standard deviation is 11.5 ounces. Bas

Question

You measure 20 turtles’ weights, and find they have a mean weight of 45 ounces. Assume the population standard deviation is 11.5 ounces. Based on this, what is the maximal margin of error associated with a 90% confidence interval for the true population mean turtle weight. Give your answer as a decimal, to two places

in progress 0
King 4 years 2021-08-25T09:52:26+00:00 1 Answers 34 views 0

Answers ( )

  1. Dulcie
    0
    2021-08-25T09:53:36+00:00
    Reply

    Answer: the maximal margin of error associated with a 90% confidence interval for the true population mean turtle weight = 4.23

    Step-by-step explanation:

    Formula for margin of error :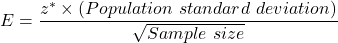 E=\dfrac{z^*\times (Population\ standard\ deviation)}{\sqrt{Sample\ size}}

    , where z* = Critical z-value.

    Given: population standard deviation = 11.5 ounces

    Sample size = 20

    Z value for 90% confidence level = 1.645

    margin of error (E) =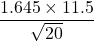 \dfrac{1.645\times11.5}{\sqrt{20}}

    \approx4.23

    Hence, the maximal margin of error associated with a 90% confidence interval for the true population mean turtle weight = 4.23

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )