Share
The distribution of resistance for resistors of a certain type is known to be normal, with 10% of all resistors having a resistance exceedin
Question
The distribution of resistance for resistors of a certain type is known to be normal, with 10% of all resistors having a resistance exceeding 10.256 ohms and 5% having a resistance smaller than 9.671 ohms. What are the mean value and standard deviation of the resistance distribution? slader
in progress
0
Physics
4 years
2021-08-24T23:22:41+00:00
2021-08-24T23:22:41+00:00 1 Answers
140 views
0

Answers ( )
Explanation:
Formula for the given probability is as follows.
According to the normal table area we have,
P(z < 1.28) = 0.10
Hence,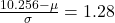
Also, the given probability is as follows.
Hence,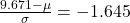
Now, substitute the value of from equation (1) into equation (2) as follows.
from equation (1) into equation (2) as follows.
Putting the value of into equation (2) we will find the value of
into equation (2) we will find the value of  as follows.
as follows.
=
= 10
Thus, we can conclude that the value of is 0.2 and the value of
is 0.2 and the value of  is 10.
is 10.