A loop circuit has a resistance of R1 and a current of 2 A. The current is reduced to 1.5 A when an additional 1.6 Ω resistor is added in se

Question

A loop circuit has a resistance of R1 and a current of 2 A. The current is reduced to 1.5 A when an additional 1.6 Ω resistor is added in series with R1. What is the value of R1? Assume the internal resistance of the source of emf is zero. Answer in units of Ω.

in progress 0
RuslanHeatt 3 years 2021-08-18T23:05:27+00:00 2 Answers 9 views 0

Answers ( )

  1. giabao
    0
    2021-08-18T23:06:40+00:00
    Reply

    Answer:

    4.8 Ω

    Explanation:

    From Ohm’s Law,

    Using,

    I = E/(R+r)…………….. Equation 1

    E = I(R+r)…………….. Equation 2

    Where I = current, E = emf, R = external resistance, r = internal resistance

    Given: I = 2 A, R = R1, r = 0 Ω

    Substitute into equation 2

    E = 2(R1)

    E = 2R1.

    When an additional 1.6 Ω  resistor is added in series,

    E = 1.5(R1+1.6)

    2R1 = 1.5R1+2.4

    2R1-1.5R1 = 2.4

    0.5R1 = 2.4

    R1 = 2.4/0.5

    R1 = 4.8 Ω

  2. thuthuy
    0
    2021-08-18T23:06:51+00:00
    Reply

    Answer:

    R1 = 4.8Ω

    Explanation:

    The loop circuit has an initial voltage of  V = IR

    I = 2 A , R1 = R

    V = 2R1

    with the current reduced to 1.5A with an additional 1.6Ω resistor

    the total resistance of the circuit is 1.6 + R1

    the voltage of the two scenarios has to be equal , since the same voltage flows through the circuit

    therefore V = 2R1

    from Ohms law V = IR

    2R1= 1.5 (1.6 + R1)

    2R1 = 2.4 + 1.5R1

    collecting like terms

    2R1 – 1.5R1 = 2.4

    0.5R1 = 2.4

    R1 =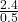 \frac{2.4}{0.5}

    R1 = 4.8Ω

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )