write a recursive formula for the following sequence 25,43,61,79,97 F(1)= 25 F(n)= F (n-1) +18

Question

Question

write a recursive formula for the following sequence 25,43,61,79,97
F(1)= 25
F(n)= F (n-1) +18

in progress 0

Mathematics Thu Thủy 4 years 2021-08-28T00:17:54+00:00 2021-08-28T00:17:54+00:00 1 Answers 5 views 0

Answers ( )

Name*

E-Mail*

Website

Featured image

Browse

Captcha* Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )

Answer*

sori · Answer 1 · 2021-08-28T00:19:06+00:00

Given:

The sequence is:

25,43,61,79,97

To find:

The recursive formula for the given sequence.

Solution:

We have,

25,43,61,79,97

Here, the first term is 25. Now, the differences between the two consecutive terms are:

$43-25=18$

$61-43=18$

$79-61=18$

$97-79=18$

The differences between the two consecutive terms is common, i.e., 18. So, the given sequence is an arithmetic sequence.

The recursive formula of an arithmetic sequence is:

$F(n)=F(n-1)+d$

Where, d is the common difference and F(1) is the first term.

Putting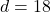 $d=18$ , we get

$F(n)=F(n-1)+18$ , where $F(1)=25$ .

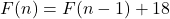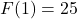Therefore, the required recursive formula is $F(n)=F(n-1)+18$ , where $F(1)=25$ .