Share
Which equation of the solutions of x2 = -7x – 8
Question
Which equation of the solutions of x2 = -7x – 8
in progress
0
Mathematics
4 years
2021-08-30T12:10:07+00:00
2021-08-30T12:10:07+00:00 2 Answers
13 views
0

Answers ( )
Answer:
Step-by-step explanation:
Answer:
x = 1, -5.56
Step-by-step explanation:
x^2 = -7x – 8
shift -7x and -8 to the other side . Remember when u shift minus changes into plus.
x^2 + 7x + 8 = 0
using quadratic equation formula
in quadratic equation one value comes positive and other comes in negative
a = 1 , b = 7 and c = 8
taking positive sign
x = (-b +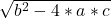 ) /2*a
) /2*a
x = (-7 +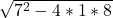 ) /2*1
) /2*1
x = (-7 +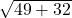 ) /2
) /2
x = (-7 +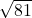 )/ 2
)/ 2
x = -7 + 9 / 2
x = 2/2
x = 1
taking negative sign
(-b –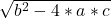 ) /2*a
) /2*a
x = (-7 –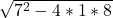 ) /2*1
) /2*1
x = (-7 –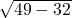 ) /2
) /2
x = -7 –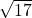 / 2
/ 2
x = -7 – 4.12 / 2
x = -11.12/2
x = -5.56
therefore x = 1 , – 5.56