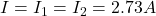Two resistors, R1 = 2.81Ω and R2 = 5.97Ω , are connected in series to a battery with an EMF of 24.0V and negligible internal resistance. F

Question

Two resistors, R1 = 2.81Ω and R2 = 5.97Ω , are connected in series to a battery with an EMF of 24.0V and negligible internal resistance. Find the current I1 through R1 and the potential difference V2 across R2 .

in progress 0
Dulcie 4 years 2021-09-05T11:21:35+00:00 1 Answers 8 views 0

Answers ( )

  1. Calantha
    0
    2021-09-05T11:23:05+00:00
    Reply

    Answer:

    2.73 A,16.3 V

    Explanation:

    R_1=2.81\Omega

    R_2=5.97\Omega

    E=24 V

    When internal resistance is negligible

    Then, V=E=24 V

    In series

    R=R_1+R_2

    Using the formula

    R=2.81+5.97=8.78\Omega

    V=IR

    24=I(8.78)

    I=\frac{24}{8.78}=2.73 A

    In series , current flowing through each resistance remains same and potential across each resistor is different.

    Therefore, I=I_1=I_2=2.73 A

    V_2=IR_2

    V_2=2.73\times 5.97=16.3 V

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )