Two quadratic functions are given. ()=−2−2+6 ()=22+5+3 Identify all values of x, to the nearest tenth, for which f (x) = g(x). A. –2.7 B. –1

Question

Two quadratic functions are given. ()=−2−2+6 ()=22+5+3 Identify all values of x, to the nearest tenth, for which f (x) = g(x). A. –2.7 B. –1.8 C. –0.6 D. 0.4 E. 4.1 F. 5.1 G. 7.0

in progress 0
Nho 4 years 2021-08-05T20:39:04+00:00 1 Answers 15 views 0

Answers ( )

  1. trucchi
    0
    2021-08-05T20:40:59+00:00
    Reply

    Answer:

    (a)\ x = 0.4\ or\ (d)\ x = -2.7

    Step-by-step explanation:

    Given

    f(x) = -x^2 - 2x +6

    g(x) = 2x^2 + 5x + 3

    Required

    Find x if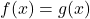 f(x) = g(x)

    The above implies that:

    -x^2 -2x +6 = 2x^2 + 5x +3

    Collect like terms

    2x^2 + x^2 + 5x + 2x + 3 - 6 = 0

    3x^2 + 7x - 3 = 0

    Using quadratic formula, we have;

    x = \frac{-b \± \sqrt{b^2 - 4ac}}{2a}

    Where

    a=3; b=7; c=-3

    x = \frac{-7 \± \sqrt{7^2 - 4*3*-3}}{2*3}

    x = \frac{-7 \± \sqrt{49+ 36}}{6}

    x = \frac{-7 \± \sqrt{85}}{6}

    x = \frac{-7 \± 9.22}{6}

    Split

    x = \frac{-7 + 9.22}{6}\ or\ x = \frac{-7 - 9.22}{6}

    x = \frac{2.22}{6}\ or\ x = \frac{-16.22}{6}

    x = 0.4\ or\ x = -2.7 — approximated

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )