Tthe diagonals of a rectangle are twice as long as the shorter sides. calculate the angle between a diagonal and a short side.

Question

Tthe diagonals of a rectangle are twice as long as the shorter sides. calculate the angle between a diagonal and a short side.

in progress 0
Thiên Thanh 4 years 2021-07-31T10:45:36+00:00 1 Answers 22 views 0

Answers ( )

  1. thucuc
    0
    2021-07-31T10:47:14+00:00
    Reply

    Answer:

    30°

    Step-by-step explanation:

    Let the length of shorter side of rectangle be x units.

    Therefore, length of diagonal = 2x

    In order to calculate the angle between a diagonal and a short side, we need to find the sin ratio of shorter side and diagonal of rectangle.

    Let the measure of angle formed between shorter side and diagonal be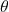 \theta .

    \therefore \sin \: \theta = \frac{x}{2x} \\ \\ \therefore \sin \: \theta = \frac{1}{2} \\ \\\therefore\sin \: \theta = \sin \: 30 \degree \\ ( \because \: \sin \: 30 \degree = \frac{1}{2}) \\ \implies \: \huge \red{ \boxed{\therefore\theta = 30 \degree }}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )