Share
Tides The length of time between consecutive high tides is 12 hours and 25 minutes. According to the National Oceanic and Atmospheric Admini
Question
Tides The length of time between consecutive high tides is 12 hours and 25 minutes. According to the National Oceanic and Atmospheric Administration, on Saturday, April 26, 2014, in Charleston, South Carolina, high tide occurred at 6:30 am (6.5 hours) and low tide occurred at 12:24 pm (12.4 hours). Water heights are measured as the amounts above or below the mean lower low water. The height of the water at high tide was 5.86 feet, and the height of the water at low tide was − 0.38 foot.
(a) Approximately when will the next high tide occur?
(b) Find a sinusoidal function of the form
y = A sin(ωx – ϕ) + B
that models the data.
(c) Use the function found in part (b) to predict the height of the water at 3 pm on April 26, 2014.
in progress
0
Mathematics
4 years
2021-07-20T20:53:45+00:00
2021-07-20T20:53:45+00:00 1 Answers
8 views
0

Answers ( )
Answer:
(a) The next tide will occur at 6:55pm
(b)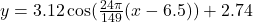
(c) The height is: 2.904ft
Step-by-step explanation:
Given
Solving (a): The next time a high tide will occur
From the question, we have that:
The next time it will occur is the sum of High and T1
i.e.
Add the minutes
Add the hours
Solving (b): The sinusoidal function
Given
The sinusoidal function is represented as:
Where
Convert to hours
Simplify
As improper fraction
Rewrite as:
So, we have:
Solving (c): The height at 3pm
At 3pm, the value of x is:
So, we have: